Python: 部品故障予測に関する計算
1. 目的
ある期間においてpの確率で故障する部品がn個稼働している。
このとき、期間内の故障発生回数が累計m回よりも多い確率を求めたい。
2. 前提条件
・故障が発生したら、その部品はすぐに新しい部品と交換される。(交換に要する時間は考慮しない)
・交換した部品が故障することもある。その場合も故障回数が加算される。
・故障の発生はポアソン分布とする。
3. 考察
1個の部品の故障率をλとする場合、この部品が期間内にx回故障する確率 P(x) は
ポアソン分布の定義から以下の式で表される。
※e は数学定数の一つであるネイピア数(Napier's constant)を表す。e = 2.71828…
※n! は n の階乗を表す。n! = n × (n-1) × ・・・ × 3 × 2 × 1
部品数がn個になれば、故障の確率はn倍となる。
したがって、故障率pのn個の部品の故障回数の累計がちょうどx回になる確率は以下ように求められる。
さて、ここで累計m回よりも多く故障が発生する確率(Q)は
1-(故障発生回数がm回以下である確率)
と計算できる。つまり、
故障が一度も発生しない確率(=故障発生回数が0)
1回だけ故障が発生する確率
累計2回故障が発生する確率
累計3回故障が発生する確率
・・・
累計m回故障が発生する確率
の合計を1から差し引いた値が求める確率である。
式で表すとこのようになる。
上記の計算を素直に実装すると、階乗の計算が m+1 回発生することとなる。
階乗自体の計算量はO(m)なので、全体の計算量はO(m2)。
mの数値が小さければ問題ないが、10000 程度なら計算不能となってしまうだろう。
式(1)をよく見ると、以下の漸化式が成り立つことがわかる。
これを利用してDP(Dynamic Programming/動的計画法)を行えば、計算量はO(m)となる。
さらに、このDPは2つの変数を交互に使用することで再利用可能である。
そうすることでメモリ使用量を大幅に節約できる。
これを擬似コードで書くと以下のようになる。
4. コード
・関数定義
import math
def FailureProbability(rate, num, times):
rate *= num
dp = [math.exp(-rate), 0]
ret = 1 - dp[0]
for i in range(1, times + 1):
dp[i & 1] = dp[i & 1 ^ 1] * rate / i
ret -= dp[i & 1]
return ret
・実行例
print FailureProbability(0.03, 18, 0) print FailureProbability(0.03, 18, 1) print FailureProbability(0.03, 18, 2) print FailureProbability(0.03, 18, 3)
(実行結果)
0.417251747626 0.102567691344 0.0176029961479 0.00230935101263
この例では、故障率3%の部品が18個稼動している場合を想定している。
この結果から、
41.7%の確率で少なくとも1個の部品が期間内に故障してしまう
予備部品を2個用意したとしても、1.76%の確率で予備部品不足となる
(3回以上の故障が発生する)
というようなことが見て取れる。

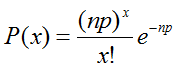


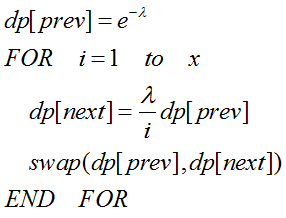
0 件のコメント:
コメントを投稿