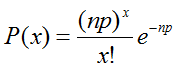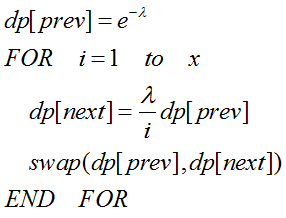C++: 自然数の分割を列挙する
正の整数 n の分割(integer partition)とは、与えられた正整数 n を正整数の和として表す方法をいう。
例えば、「6」 はこのように11通りの異なる方法で分割できる。
6 5+1 4+2 4+1+1 3+3 3+2+1 3+1+1+1 2+2+2 2+2+1+1 2+1+1+1+1 1+1+1+1+1+1
この成分(part)の組み合わせを std::vector<int> として順次生成するクラスを作りたい。
以下、この関数を P(n) と呼ぶ。
1. 再帰を利用したアルゴリズム(Python)
Python のジェネレータ機能を使ったコードが、こちらに投稿されている。
http://code.activestate.com/recipes/218332-generator-for-integer-partitions/
処理時間計測用のコードと併せて記載する。
def P(n):
# base case of recursion: zero is the sum of the empty list
if n == 0:
yield []
return
# modify partitions of n-1 to form partitions of n
for p in P(n - 1):
p.append(1)
yield p
p.pop()
if p and (len(p) < 2 or p[-2] > p[-1]):
p[-1] += 1
yield p
def main():
import timeit
for n in (15, 30, 45, 60, 75, 90):
code = 'for _ in P(%d): pass' % n
print 'n=%d elapsed=%f' % (
cnt,
timeit.Timer(code, 'from __main__ import P').timeit(1))
if __name__ == '__main__':
main()
手元のPC(Intel Core2Duo E4600 @ 2.40GHz)での実行結果は以下のとおり。(処理時間の単位は秒)
n=15 elapsed=0.000423 n=30 elapsed=0.015092 n=45 elapsed=0.290839 n=60 elapsed=3.473330 n=75 elapsed=31.071480 n=90 elapsed=236.823416
このコードのアルゴリズムは以下のようになる。
①P(n) の計算にあたり、P(n-1) を列挙する。 ※P(0) は空のリストを返す。
②P(n-1) の各出力に対して、末尾に新規の成分「1」を追加したリストを出力する。
③P(n-1) の各出力を k個の成分を持つリスト x1,x2, … ,xk とした場合、
成分の個数が1個(k=1)であれば、その唯一の成分を インクリメントする。(x1 ← x1 + 1)
末尾の2成分(xk-1, xk)について、xk-1 > xk が成立する場合、末尾の成分をインクリメントする。(xk ← xk + 1)
インクリメントしたリストを出力する。
(言い換えれば、末尾の成分をインクリメントしても要素の降順が守られる場合にのみインクリメント実行)
この結果出力される各成分は降順にソートされている。また、出力結果は辞書順となる。
P(0)~P(5) の処理の様子はこのようになる。
緑色の箇所はP(n-1)に対して新規の成分「1」を追加したこと、ピンク色の箇所は既存の成分をインクリメントしたことを表している。
2. 再帰を利用しないアルゴリズム(C++)
以下の文献を参考に、C++で処理を実装してみる。
Antoine Zoghbiu and Ivan Stojmenovic. Fast Algorithms for Generating Integer Partitions. Intern. J. Computer Math., 70, 319-332 (1998) (PDF)http://www.site.uottawa.ca/~ivan/F49-int-part.pdf
出力は辞書の逆順とするほうがコストが小さい。そのアルゴリズムはこのような感じだ。
尚、この場合も1つの出力における各成分は降順にソートされるようにする。
①n = 0 の場合は空のリストを出力して終了。
②成分が1個だけのリスト {n} を作成し、それを出力する。
③2以上の成分の数を h とおき、1 を代入する。(h ← 1)
# 以下、④~⑦を繰り返す
④最初の成分が1 (x1 = 1) ならば終了。
⑤2以上の成分のうち最も右側にあるもの(xh)をデクリメントし、その値を r とする。(r ← xh-1; xh ← r)
⑥xh より右側にあった成分を全て結合し、{r, r, … , d} (0 < d ≦ r) という形に再構成する。
xh より右側の成分は、定義より全て 1 であるから、現在のリストの個数を|{x}|とすると
|{x}| h + 1 = c × r + d (0 < d ≦ r)
という変換を行えばよいことが分かる。
⑦r = 1 の場合は h をデクリメントする。(h ← h - 1)
r > 1 かつ d = 1 の場合は h に c を加算。(h ← h + c)
r > 1 かつ d ≧ 1 の場合は h に c+1 を加算する。(h ← h + c + 1)
# ④へ戻る
P(6) の処理の様子を以下に示す。
| ・リスト {n} を作成 ・h ← 1 | |
| ・xh = x1 をデクリメント ・1 を 5 単位で再構成: 1 = 0 × 5 + 1 ・2 以上の成分の個数(h)は変わらず | |
| ・xh = x1 をデクリメント ・2 を 4 単位で再構成: 2 = 0 × 4 + 2 ・2 以上の成分ができたので h を増加 | |
|
・xh = x2 をデクリメント | |
|
・xh = x1 をデクリメント | |
|
・xh = x2 をデクリメント | |
|
・xh = x2 をデクリメント | |
|
・xh = x1 をデクリメント | |
|
・xh = x3 をデクリメント | |
|
・xh = x2 をデクリメント | |
|
・xh = x1 をデクリメント ・これで、最初の成分(x1)が 1 になったので終了 |
黄色の箇所は 2以上の数値(=h としてカウントされるもの)を、青色の箇所はデクリメントした結果1となったこと(=hのデクリメントを伴ったこと)を表している。
コーディングにあたっては、簡単のため h を 1-indexed から 0-indexed へ変換する。
xh = 2 のときの再配分処理はリストの末尾に 1 を追加するだけでよい。
また、出力したリストの個数を count 変数として保持することにした。
今回もやはり時間計測用のコードと一緒に掲載する。
#include <vector>
#include <ctime>
#include <cstdio>
// Generator for integer partition.
class Partition {
public:
int count;
Partition(int n) {
x_ = std::vector<int>(std::min(1, n), n);
h_ = n > 1 ? 0 : -1;
count = 0;
}
std::vector<int> &next() {
if (x_.empty()) return x_;
if (count > 0) {
if (h_ < 0) {
x_.clear();
return x_;
}
if (x_[h_] == 2) {
--x_[h_--];
x_.push_back(1);
}
else {
int r = --x_[h_];
int t = x_.size() - h_;
while (t >= r) {
x_[++h_] = r;
t -= r;
}
if (t == 0) {
x_.resize(h_ + 1);
}
else {
x_.resize(h_ + 2, 1);
if (t > 1) x_[++h_] = t;
}
}
}
++count;
return x_;
}
private:
std::vector<int> x_;
int h_;
};
int main() {
// Print each P(6).
Partition p(6);
std::vector<int> v;
while ((v = p.next()).size()) {
printf("%2d: [", p.count);
for (int i = 0; i < (int)v.size(); ++i) {
printf("%s%d", i == 0 ? "" : ", ", v[i]);
}
printf("]\n");
}
// Measuring time elapsed.
int n[] = {15, 30, 45, 60, 75, 90};
for (int i = 0; i < static_cast<int>(sizeof(n) / sizeof(n[0])); ++i) {
clock_t t = clock();
Partition p(n[i]);
while (p.next().size()) {}
clock_t s = clock();
printf("n=%d elapsed=%.6f count=%d\n", n[i],
static_cast<double>(s - t) / CLOCKS_PER_SEC, p.count);
}
return 0;
}
実行結果は以下のとおり。(処理時間の単位は秒)
1: [6] 2: [5, 1] 3: [4, 2] 4: [4, 1, 1] 5: [3, 3] 6: [3, 2, 1] 7: [3, 1, 1, 1] 8: [2, 2, 2] 9: [2, 2, 1, 1] 10: [2, 1, 1, 1, 1] 11: [1, 1, 1, 1, 1, 1] n=15 elapsed=0.000000 count=176 n=30 elapsed=0.000000 count=5604 n=45 elapsed=0.010000 count=89134 n=60 elapsed=0.105000 count=966467 n=75 elapsed=0.818000 count=8118264 n=90 elapsed=5.612000 count=56634173
参考:
http://handasse.blogspot.com/2010/01/blog-post.html
Wikipedia
http://en.wikipedia.org/wiki/Partition_%28number_theory%29
http://ja.wikipedia.org/wiki/%E8%87%AA%E7%84%B6%E6%95%B0%E3%81%AE%E5%88%86%E5%89%B2