IVA読書会 chap01-sect03 宿題
Ideals, Varieties, and Algorithms 読書会 #3 - PARTAKE の宿題、担当分に挑戦してみる。
No.5
双曲線 $x^2 - y^2 = 1$ に関する問題
a.
$$ x = \cosh(t) = \frac{e^t + e^{-t}}{2} \\ y = \sinh(t) = \frac{e^t - e^{-t}}{2} $$
$x^2 - y^2 = {(\frac{e^t + e^{-t}}{2})}^2 - {(\frac{e^t - e^{-t}}{2})}^2$ を計算すると 1 となる。
$t$ に関わらず成立するので、これらの点は $x^2 - y^2 = 1$ 上に常に存在する。
また、定義から $x = \cosh(t) \gt 0$ であるため、双曲線うち右側の曲線(第1, 第4象限)のみカバーされる。
b.
ヒントにあるように、場合分けして考える。
(1) x = a の場合
代入して a^2 - y^2 = 1 を y について解く
(i) -1 < a < 1 のとき交点なし
(ii) a = ±1 のとき交点は1つ
(iii) a < -1 または 1 < a のとき交点は2つ
(2) y = mx + b の場合
代入して x^2 - (mx + b)^2 = 1 という方程式の解の個数について考える
展開すると (1 - m^2)x^2 - 2mbx - (1 + b^2) = 0
(i) m = ±1 のときは x についての一次方程式となり、x = ±((1 + b^2) / 2b) が得られる
b = 0 のとき交点なし
b ≠ 0 のとき交点は1つ
(ii) m ≠ ±1 のときは二次方程式となるため、その判別式Dを考える
D = 4 m^2 b^2 + 4 - 4m^2 + b^2 - 4m^2 b^2 = 4(-m^2 + b^2 + 1)
m^2 - b^2 > 1 のとき交点なし
m^2 - b^2 = 1 のとき交点は1つ
m^2 - b^2 < 1 のとき交点は2つ
まとめると、
交点なし
x = a (-1 < a < 1)
y = x
y = -x
y = mx + b (m ≠ ±1, m^2 - b^2 > 1)
交点1個
x = -1
x = 1
y = x + b (b ≠ 0)
y = -x + b (b ≠ 0)
y = mx + b (m ≠ ±1, m^2 - b^2 = 1)
交点2個
x = a (a < -1, 1 < a)
y = mx + b (m ≠ ±1, m^2 - b^2 < 1)
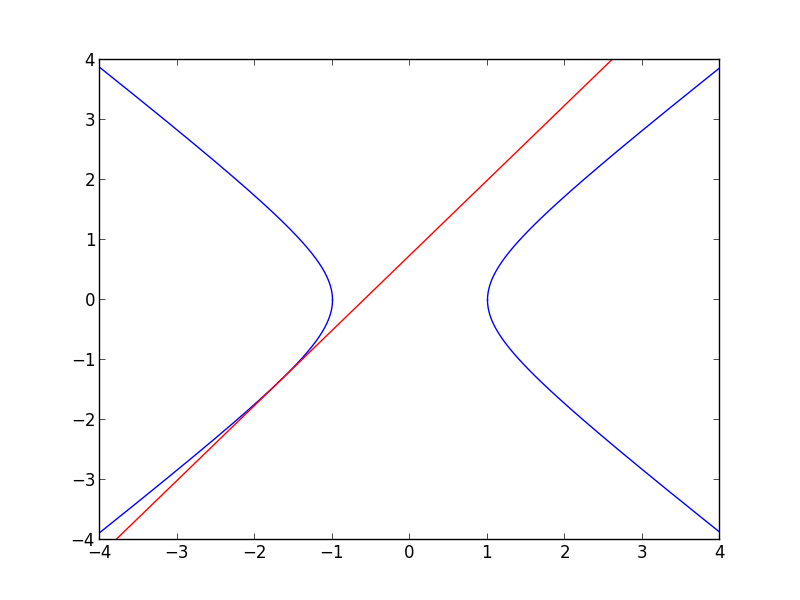
y = 1.25x + 0.75 の例 (交点1個)
c.
(-1, 0) および (0, t) を通る直線を考え、双曲線の右側との交点を (x, y) とすると、
1 : t = 1 + x : y より
y = t(1 + x) が求められる。
これを x^2 - y^2 = 1 に代入して解くと
x = (1 + t^2) / (1 - t^2)
y = 2t / (1 - t^2)
が求められる。
d.
双曲線 x^2 - y^2 = 1 の漸近線は y = ±x である。
t = ±1 のとき、直線の傾きが漸近線と並行になるため、(-1, 0) 以外の交点を持たない。
No.11
a.
ex.08-d の式の y を x, x を z に置き換える。
b.
c を y^2 に置き換えると、
x^2 = y^2 z^2 - z^3 となり、これは x^2 - y^2 z^2 + z^3 = 0 を表す。
c.
考え中。
(0, 0), (x, y), (1, t) を通る直線を考える?
No.17
(x1, y1) = (1, 0)
(x2, y2) = (1, 1)
(x3, y3) = (0, 1)
というベジエ曲線であると捉える。
a = 1 - √2 / 2
b = √2 - 1
w = 1 / √2
が求まるので、これらの値をex.16の式に代入すればよい。
x = ((1-t)^2 + √2 t(1-t) ) / ((1-t)^2 + √2 t(1-t) + t^2)
y = ( √2 t(1-t) + t^2) / ((1-t)^2 + √2 t(1-t) + t^2)
TeX系の表示環境がないとつらい・・・
0 件のコメント:
コメントを投稿